本文的作者是 Peta Hung
他在臉書社團分享這篇文章,大仁看了獲益良多。
裡面談到資產配置與槓桿 ETF 的相關討論。
雖然數字細節我沒有核對,但過程跟結論,都與我多年來的研究經驗相符。
對於想用槓桿 ETF 做為投資組合的朋友,非常值得參考。
在徵詢作者同意後,將文章轉載上來,讓更多人可以從中受益。
內文完全沒有更動,只有將排版與一些標點符號重新順過。
有涉及比較專業的地方,可以放慢速度多看幾次。
日後,大仁也會針對這部份的主題做相關分享。
閱讀愉快。

前言
過去歷史的演變過程,僅僅是隨機程序中的一種情境。
想要探討一個隨機事件各種發展路徑的結果,採用蒙地卡羅模擬(Monte Carlo simulation)是非常良好的工具。
下文蒙地卡羅模擬的樣本來源起始年份是 2008 年初,這是因為受限於二倍槓桿基金 QLD 的發行年份。
結尾年份是 2022 年末,而非 2023 年末,是為了避免過於樂觀的結果。
以下觀察的重點會是平均年化成長率(Compound annual growth rate, CAGR),以及最大回撤比例(Maximum draw down, MDD),並且數字都不經過通貨膨脹率調整。
投資的長期風險來自於過低的 CAGR,若是績效不彰甚至落後於長期通貨膨脹率,這將會導致實質購買力縮水,最終社會階級向貧窮方向滑落。
投資的短期風險來自於過高的 MDD,巨幅的回撤若是導致投資信心不足,進而出脫資產將會造成永久損失。
此外,若是現金流的來源仰賴已投資資產,除了下跌造成巨大心理壓力外,若是執行股票質押借款,則可能因為跌幅過大,而被資金提供方給強迫清盤離場!
本文為整理 portofolio visualizer 的模擬結果,為了方便比較,故採箱形圖(box chart)呈現。
其中盒子的下緣、上緣分別是第一四分位數(1st quatile, Q1)、第三四分位數(3rd quatile, Q3),中間的橫線為中位數(median)。
盒子的下延伸線、上延伸線的邊緣分別是第 10 百分位數(10th percentile)、第 90 百分位數(90th percentile)。
直觀來說,由下而上五個標記點分別表示五種發展路徑。
各自呈現最倒楣的投資人、不太幸運的投資人、普通的投資人、幸運的投資人,和最幸運的天選之人他們的投資成果。
雖然箱形圖可以方便各資產、不同持有時長之間的對比,但是箱形圖無法呈現出模擬結果之機率分佈的真實情況。
幸虧箱形圖還是足以幫助我們瞭解一些數據的特性,包括觀察盒子的寬度也就是四分位距(inter-quatile range, IQR)反映了數據的變異性。
另外觀察中位數是否位於盒子中心、盒子距離上下延伸線邊緣是否等距離,都可以反映數據的分佈是否具有偏態。
最後,必須強調蒙地卡羅模擬無法得知未來所有的發展結果,只能顯示出未來可能的許多種發展結果,所以箱形圖中每個節點的實際數值並不重要。
重點是各種資產類別或是組合的比較,以及不同持有時長的比較,從這些比較中獲得一些啟發。
此外模擬的輸出極受原始樣本的分佈傾向所影響,所以接下來會先以 SPY 的歷史資料,對比模擬結果以評價模擬的可靠性。
SPY vs TLT vs CASH
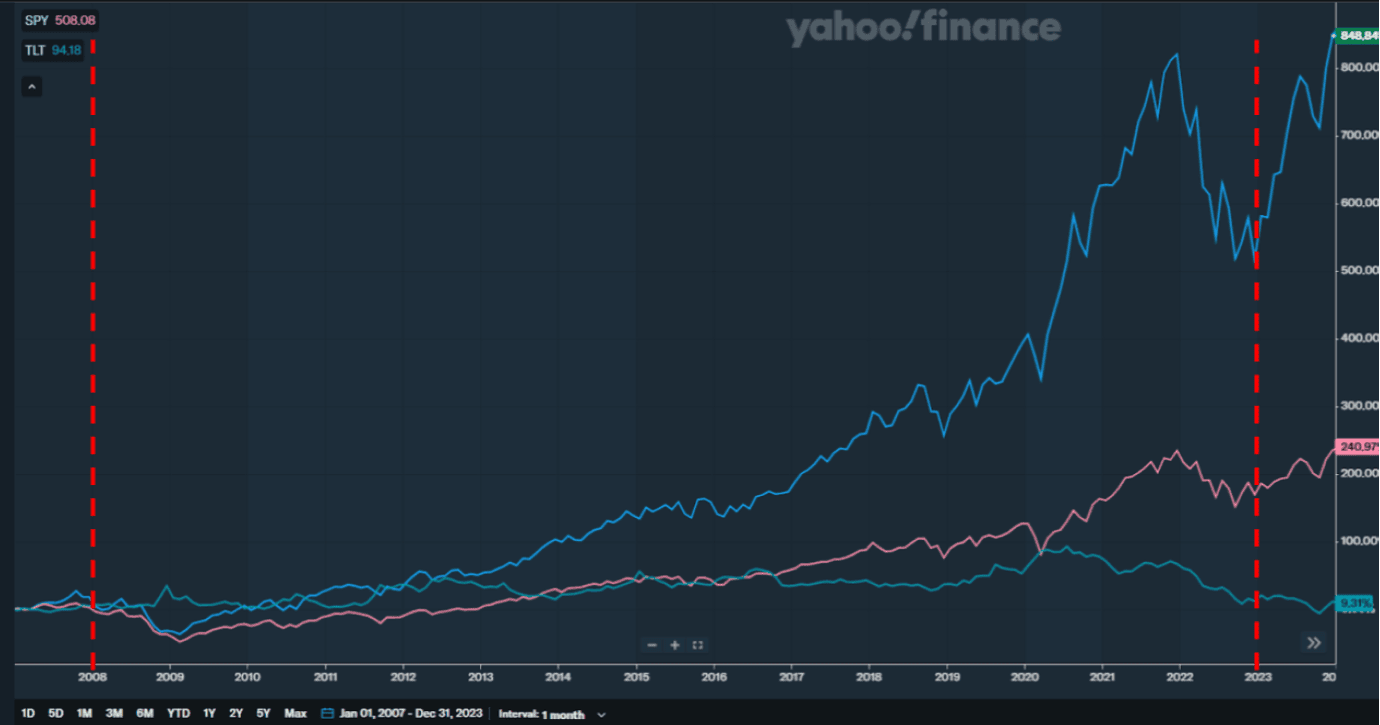
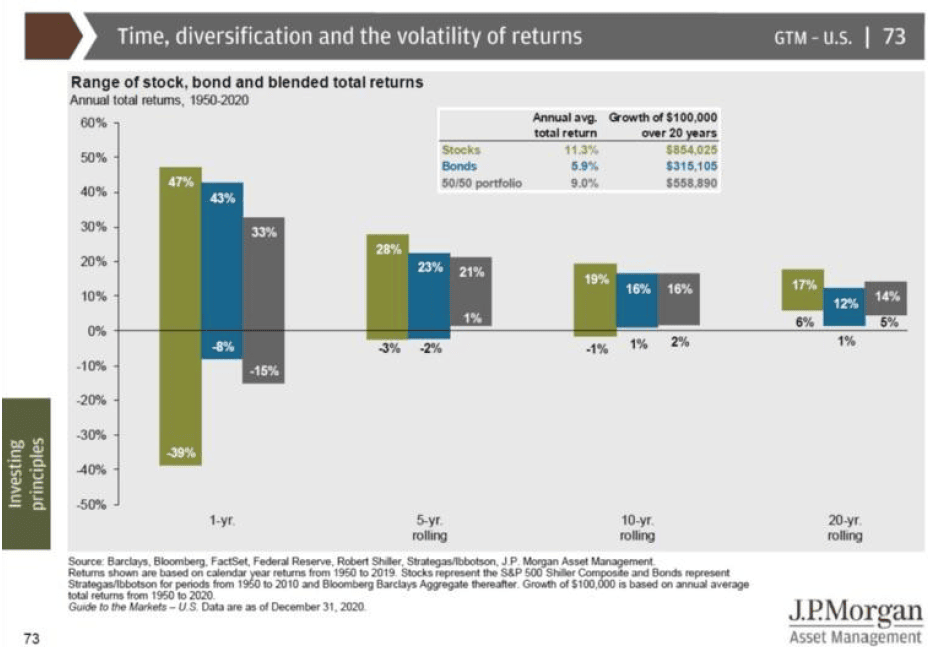
首先觀察下圖 JPMorgan 提供 1950-2020 之歷史資料。
草綠色的股市回報率分佈不論滾動 5 年、滾動 10 年、滾動 20 年。
基本上都涵蓋於圖一(a)中 SPY 的 CAGR 箱形圖(含延伸線)内。
由此推斷取 2008 年初至 2022 年末的資料作為模擬分析的母數,不失廣泛適用性而具有參考價值。
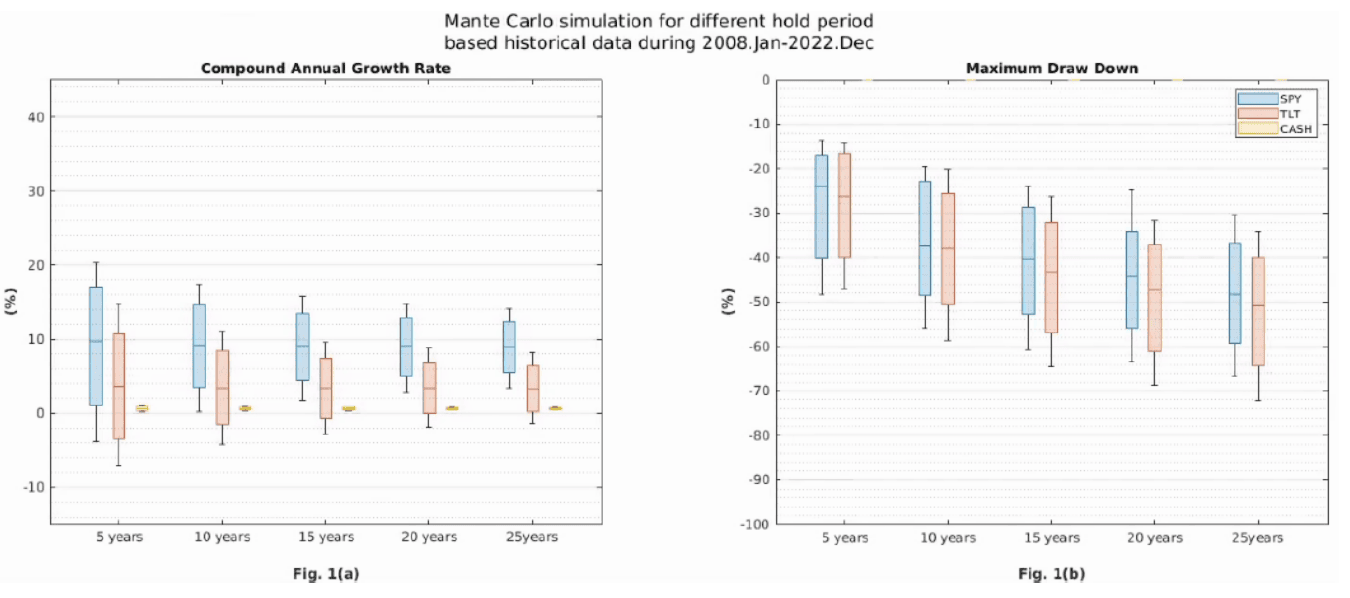
圖一首先可以觀察到 CASH(定期存款、1-3 月短期國庫券)
最特別的就是,不論持有時長多少,其 MDD 恆為 0。
因為這特性相較於投資股票需承受可能下跌的不確定性,也就不難理解為何許多人寧可持有現金而不投資。
但是持有大部位現金而不願意積極投資的風險趨避者,其實忽視了難以承擔的長期風險—過低的 CAGR
避開短期風險其實也必將錯失回報,變相將自己推向貧窮的一端。
接下來觀察 SPY,可以注意到只要持有超過 15 年,即使是模擬結果 CAGR 其中最惡劣的 10%,也能擁有正報酬。
此外,也可以發現投資成果的變異性(最佳回報與最差低回報的落差),經由拉長投資年限將會使之顯著縮窄:
最好的結果會逐漸向下收斂、最差的結果會逐漸向上靠攏。
這說明了投資是公平的,最幸運的投資者和最倒楣的投資者,經過逐漸加長的投資年限,他們二者之間可以獲得的平均回報差距應該可以小到令所有人滿意。
另外 SPY 的 MDD,隨著時間增加則可能遭遇的跌幅也越大,而投資人正是因為勇於承擔這樣的下跌而獲得回報。
例如 SPY 持有 25 年的期間,若市況不佳則可能的MDD超過 -60%
但無論是投資 25 年的初期或是後期遭遇這樣的跌幅,終究 CAGR 依然約有 4%
可見無論何時,下跌絕不是賣出股票的原因。
在圖一當中,最令人感到詫異的是,長期債券基金 TLT 即使持有長達 25 年,依然可能有負報酬的情形。
而且除了 CAGR 的中位數僅約 4% 外,其 MDD 的箱形圖分佈整體寬幅都略大於 SPY 的 MDD
盒子也都位於更下方—更大的潛在跌幅。
TLT 的表現讓持有者同時面臨長期風險及短期風險,而無相應回報,並不是理想的投資標的。
SPY vs QQQ vs QLD
這裡想要比對 SPY 與 QQQ 及其單日二倍做多的槓桿 ETF
並且研究如果看好長期上漲,是否應該全倉投入(all-in)槓桿 ETF?
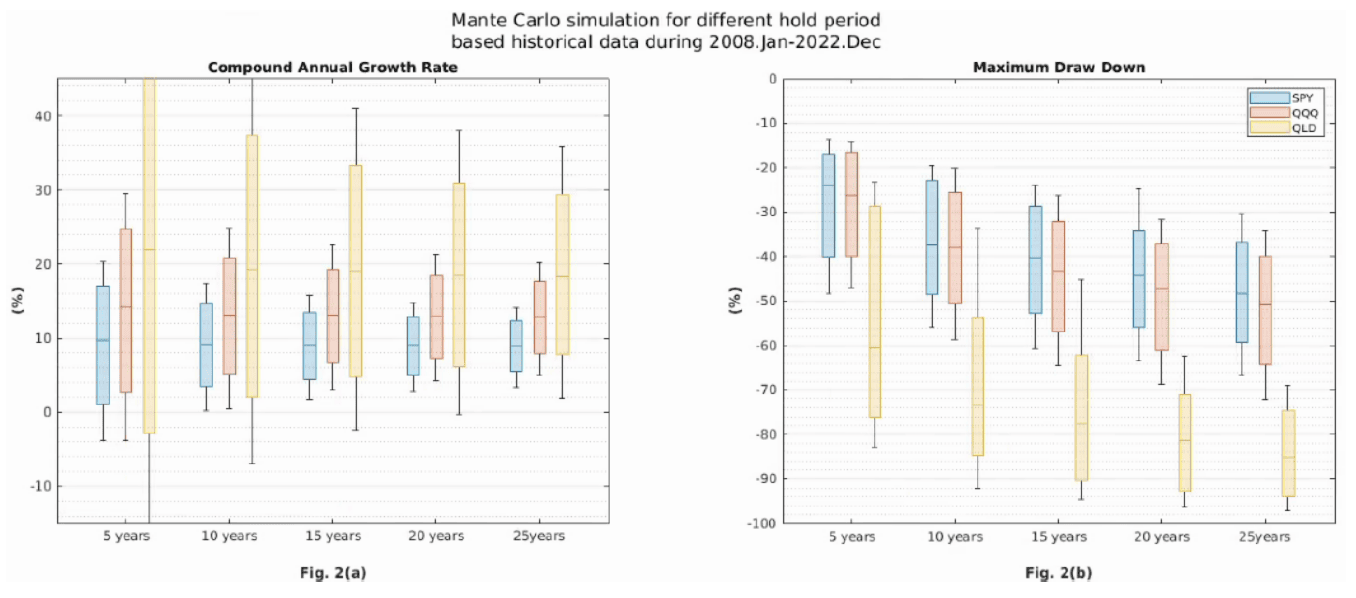
觀察圖二中,QQQ 的 CAGR 箱形圖均位於比 SPY 更上方位置(更高回報),但是 QQQ 的 MDD 箱形圖均位於略比 SPY 更下方位置(更高下挫)。
這意味著雖然二者均為分散投資從而避免非系統性風險,但 SPY 額外增加了 400 家股票仍可獲得更好的下跌保護,而若除去這額外 400 家股票則可以獲得更好的 CAGR 回報。
此外,QQQ 的盒子都略長於 SPY 的盒子,這表示機運的作用在 QQQ 上的影響,只是略高於作用在 SPY 上。
運氣差的人投資了 QQQ 而落後運氣好的人投資了 QQQ 的程度,只略高於運氣差的人投資了 SPY 而落後運氣好的人投資了 SPY 的程度。
但是運氣最差的人選擇投資了 QQQ,長期來說其平均回報優於選擇投資於 SPY。
QLD 的 CAGR 箱形圖 5 年的盒子上緣是爆表的 58% 這使得許多人趨之若鶩;
但 5 年的延伸線下緣同樣也是爆表的 -16%,這就是有人棄如敝屣的原因。
QLD 的 CAGR 盒子寬度大約都是 QQQ 的兩倍。
也就是說雖然槓桿的作用提高了平均回報的中位數,不過更是顯著提高了變異性,換言之,機運發揮的作用更明顯了。
幸運地買在低點的人將獲得無上的平均年回報率,但不幸運的人若買在泡沫頂點則即使持有長達 20 年,依舊無法得到正報酬,很難想像這會有多麼折磨投資人的心智!
雖然 QLD 的 CAGR 也有隨著拉長投資年限,而逐漸收窄變異性的趨勢,但是收斂的速度可能慢得令人無法忍耐。
另外觀察 QLD 的 MDD 箱形圖。
在 25 年的投資期間内的任意時刻內,有可能遭遇 -98% 這樣災難性的下跌,初期遇到此災難或許還能東山再起。
但若是後期才遭遇此災難那就有如走在幽暗的隧道内,不知何時才能重見陽光?
不可不慎!
此處延伸討論一點,假若各個單年分的報酬率可以視為獨立的隨機變數,那麼根據中央極限定理可以得知,長期投資下的平均(幾何平均)年回報率會是具有對數常態分配(Log-normal distribution)的隨機變數。
當採取單日二倍做多的方式放大波動率時,也必然放大平均年回報率之標準差。
這將使得原本就非對稱的分佈產生更明顯的偏態(skewness),如右圖中的藍線變成紅線就是偏度放大的結果。
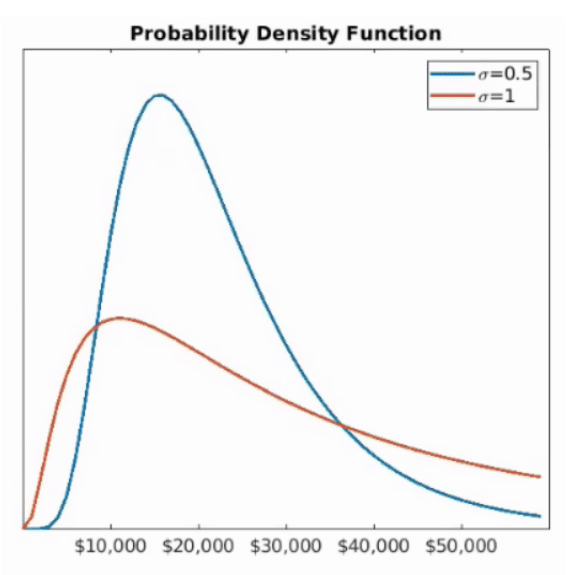
但這個預期的偏度放大並沒有在模擬中於箱形圖顯現出來。
高偏態意味少數極端事件獲得了極高的平均年回報,但是絕大多數事件發展路徑遠低於此,典型的極端案例就是樂透彩的彩金分配結果。
QQQ vs CASH vs 50/50
槓桿 ETF 的真實功用-與現金互補:
現金可彌補 QLD 的巨幅 MDD
QLD 可彌補現金差勁的 CAGR
底下營造了一種狀況,某位投資人為了某些原因而必須保留現金(作為緊急備用金、擔保品借貸等等)
那麼只要將與現金同比例的資金投入二倍槓桿 ETF
並且每年經過漲跌後,定期無腦地將槓桿 ETF 和現金重新調整回 1:1
就可以解決了現金投資效率滯後(cash drag)的問題。
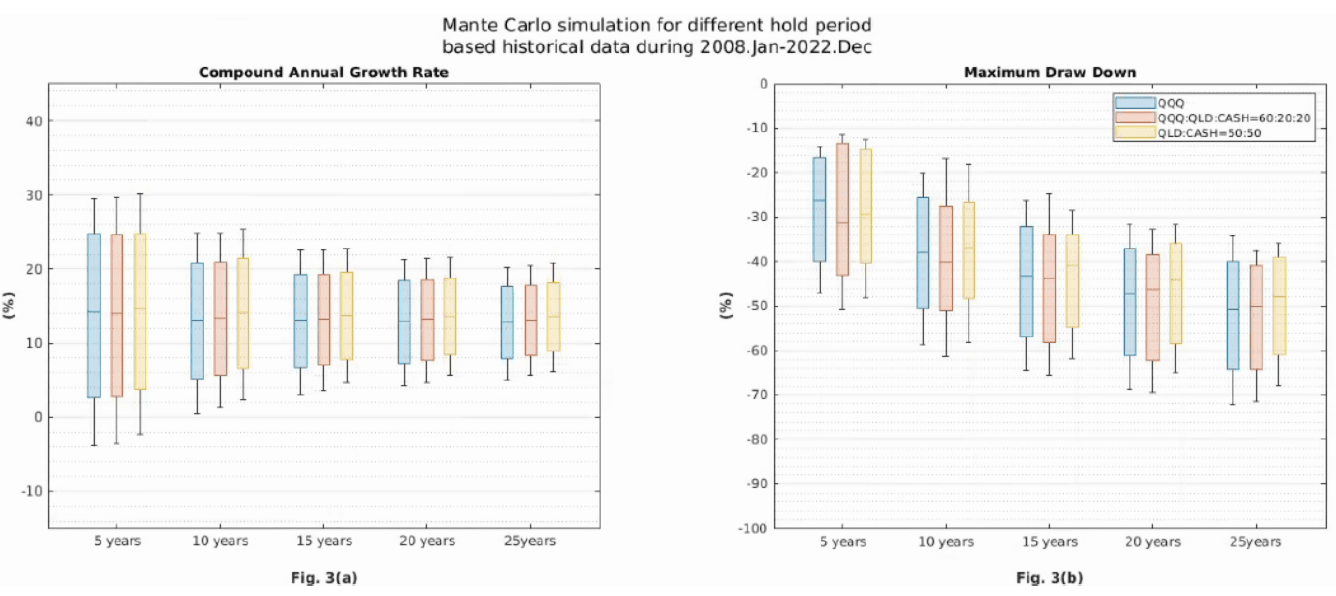
圖三的紅色箱形圖就是 QQQ:QLD:CASH = 60:20:20 的狀況,預期這樣的波動率(beta, β)正好等效於 100% QQQ 的波動率。
可以發現其 CAGR 的盒子寬度幾乎等於 100% QQQ,且盒子整體還微微地上方一些-可能有略好的平均年報酬,但這種配置狀況的 MDD 顯然繼承了來自 QLD 的特性,而具略高的 MDD 跌幅。
其實這不難明白,因為歷經連日漲跌之後,QQQ:QLD:CASH 的比例必定偏移,當 QLD 上漲時則 QLD 比例加重,這表示未來可能面臨較大跌幅,直到重新再平衡即可消除此問題。
若進一步提高現金比例呢?
按照上述規則,極限就是 QLD:CASH = 50:50
可以發現其 CAGR 的盒子寬度依然幾乎等於 100% QQQ,且盒子整體還更略為上方一些。
但是這次的 MDD 則因為現金比例提高而發揮作用,這個配置的 MDD 得到了比 100% QQQ 還小的變異性,盒子也更上方表示整體比 100% QQQ 略小的跌幅。
看起來似乎是同時得到較小短期風險、又能得到較優長期回報雙重優勢的配置方式,不過此時仍要回到源頭重新思考為何要配置如此高比例的現金呢?
高比例的現金在手可能導致各種因為貪婪/恐懼而產生的行為偏誤。
股市漲得多而想要追高、股市跌得深而想要抄底、股市跌更多而不敢依計畫再平衡;又或是隨著高比例的槓桿 ETF 部位之波動,而導致錯誤地停利或停損等等。
又即使紀律嚴明地克服了心魔,使再平衡計畫仍如預期進行,因為高比例的現金和高比例槓桿 ETF 進行再平衡,終究逃不過更高昂的交易手續費,或是包括資本利得稅。
另外,如果進行股票擔保品借貸時,需要考慮資金提供方未必可以接受以槓桿 ETF 作為擔保品,但現金、原型指數基金則較不會有這個疑慮。
QQQ vs beta1.2 vs 60/40
資訊科學家給賭徒的建議:凱利公式,這個計算原則是在已知平均回報率的期望值(扣除無風險利率)、標準差的前提下,為了獲取長期連續博弈的最高平均回報率應該下注的比例。
過去曾有研究,應用上述原則分析針對 S&P500 的建議投資比例是 117%
這表示 all-in 還不足以獲得最佳的平均年回報率,應該還要借貸以獲得額外 17% 的原始資金,在這樣的槓桿操作下才能得到預期最佳的平均年回報率。
但是借貸除了需要利息成本外,往往需要先擁有優質擔保品,或是足夠良好信用才可獲得資金,那麼是否有其他方式可以做到等效 117% 的投資呢?
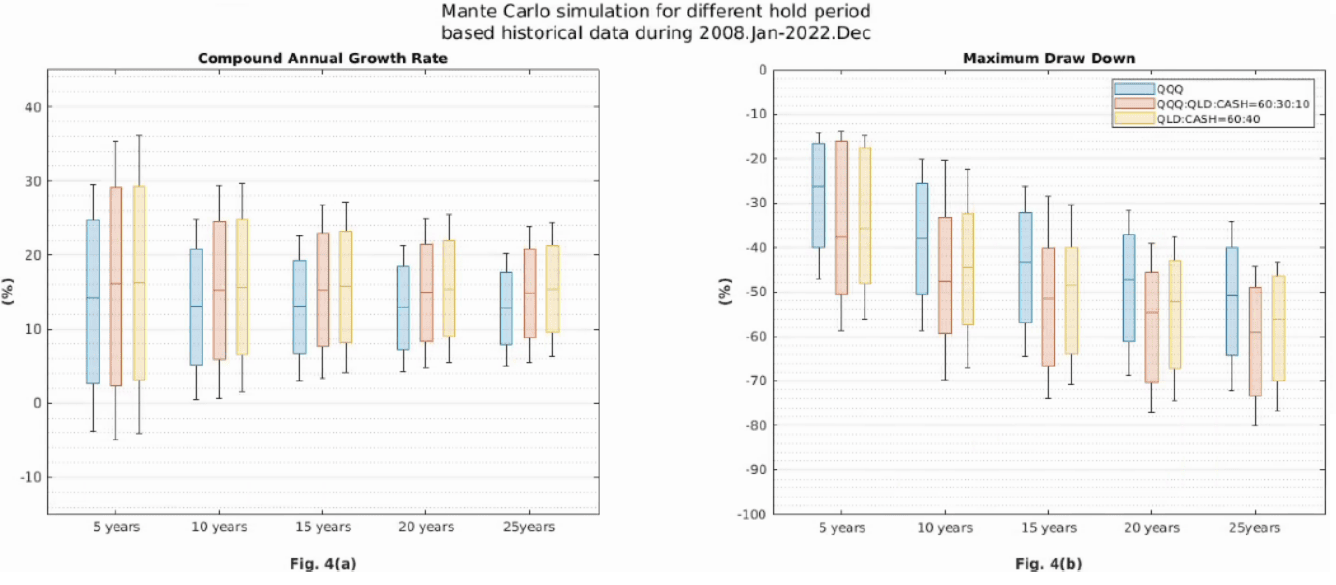
圖四的紅色 CAGR 箱形圖是依照 QQQ:QLD:CASH = 60:30:10之比例配置,預期波動率是 QQQ 的 120% 倍。
結果可以發現紅色 CAGR 中位數約比 QQQ 的 CAGR 中位數多 2%
另外超過 10 年之箱形圖下延伸線的邊緣幾乎切齊 QQQ 的下延伸線邊緣,但是箱形圖的上延伸線或盒子上緣都高過 QQQ
對此的解讀是,利用現金和二倍做多槓桿基金的比例調整,使得波動率放大之後,不但並未降低預期最低平均年報酬率,卻可以使得預期最高平均年報酬率提高,難道天下有白吃的午餐嗎?
觀察紅色 MDD 箱形圖就會發現,波動率放大之後的盒子均比原始 QQQ 還下方。
換言之,無論何時這個配置都要承受比 QQQ 高的下挫幅度,這就是想要獲得高報酬的代價。
前面一小節中,提高現金比例而減低 MDD 的效果,在此處依然有效。
在預期波動率為 120% 倍於 QQQ 時極大化現金比例,就會得到 QLD:CASH = 60:40 這樣的配置。
從 CARG 箱形圖中可以發現,黃色盒子整體約略等寬、等高於紅色盒子;
再看 MDD 箱形圖,可以看出來黃色盒子比紅色盒子位於上方,也就是說提高現金比例後,在不減損回報率的前提下,確實地減低了最大下挫幅度。
這裡可以先做出小結,槓桿基金是一個強大工具,可以用於與原型指數基金、現金做比例搭配,省去借貸或是操作其他衍生性金融商品的複雜,輕鬆就能調整到想要的槓桿倍率!
若把原型指數基金比喻為牛排,現金與槓桿基金就好比鹽巴與胡椒,適當調配會使得牛排更加美味,
但是不會有人想在牛排館單點鹽巴或是胡椒的!
QQQ vs 60/40 vs 60/40(TLT)
TLT 雖然並非總是與股市成反向關係,但是考慮其與股市長期呈低度相關,一直都是傳統股債平衡資產配置中的熱門選項。
若是用 TLT 取代配置中現金部位,會有何效益?
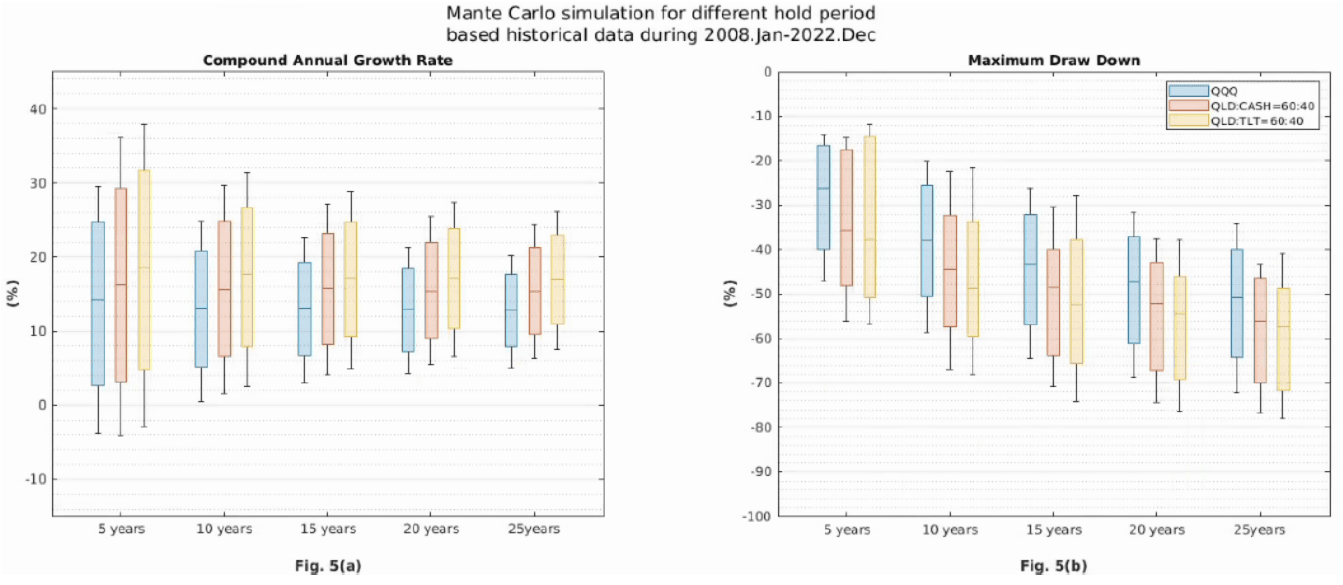
一如既往,從圖五 CAGR 的箱形圖來看,再次重現了這樣的效果:
黃色箱形圖下延伸線的邊緣切齊或高於 QQQ 的下延伸線邊緣,箱形圖的上延伸線或盒子上緣都高過 QQQ。
現金改為 TLT 之後,不但略略提高預期最低平均年報酬率,還可以使得預期最高平均年報酬率再度提高。
同樣地,天下沒有白吃的午餐,獲得更高回報的代價就是要承擔更高的 MDD-MDD 箱形圖中黃色總是比藍色、紅色還要更下方。
不論 QQQ 之於 SPY,或是 120% 波動率的配置之於原型 QQQ
以及這裡所探討 TLT 取代現金的方式,都是以較大的 MDD換取較大的 CAGR。
簡言之,高報酬必然高波動,這只是透過調整 β 對應的效益,無法有超額報酬(α)。
回到牛排的比喻,這次鹽巴(現金)換成調味鹽(TLT)
雖然使口味更美,但卻未必人人能接受的!
結語
本文首先展示了現金、TLT、QLD 各自的風險,像是包括了低成長低回報,或是高度變異性使得輸贏全憑運氣等等。
但是,這些單獨使用會有各自問題的資產類型,經過比例調配之後的組合就能得到一些十分有趣的特性。
還是回到一句老話,投資可不能看著後視鏡開車,除了凱利公式所需要的變數其實屬於未知,所以最佳的投資槓桿倍率無法得知之外;還有雖然蒙地卡羅模擬法的分析方式已經非常客觀。
但是畢竟只取了有限時間段內的數據來分析,當黑天鵝降臨時,那樣的事件往往不是資料統計上可以觀察到的!
關於投資本就千變萬化,假如加入槓桿基金就有更多可能性了!
本文旨在提出一種觀察視角,可以多增加一些背景知識,畢竟我認為投資當中,最大的危機不是下跌,而是無知造成的後果:冒了巨險而不自知,或是不知不肯冒險的下場。
最後是一旦有了資產配置,就會有再平衡的需要。
再平衡的手法也並非只能定期地、無腦地按照原始比例重新分配,可以有其他戰術性的做法。
涉及這些比較複雜的操作,模擬起來也就更為困難,那就超過在本文的分析範圍外了。
Peta Hung, 2024.10.19
延伸閱讀:【懶人包】「槓桿投資法」系列
對槓桿思維有興趣的朋友,歡迎加入臉書社團一起討論:社團連結
也可以參考大仁的最新作品:《槓桿 ETF 投資法》



